ТЕМА 17

Квадратне рівняння. 

Геометричний зміст квадратного рівняння

Графіком функції, яка представлена квадратним рівнянням є парабола. Розв'язки (корені) квадратного рівняння – це точки перетину параболи з віссю абсцис (х). З цього випливає, що є три можливі випадки:

1) парабола не має точок перетину з віссю абсцис. Це означає, що вона знаходиться верхній площині з вітками вгору або нижній з вітками вниз. В таких випадках квадратне рівняння не має дійсних коренів.

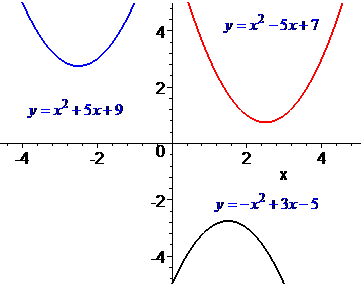
2) парабола має одну точку перетину з віссю Ох. Таку точку називають вершиною параболи, а квадратне рівняння в ній набуває свого мінімального або максимального значення. В цьому випадку квадратне рівняння має один дійсний корінь (або два однакових кореня).

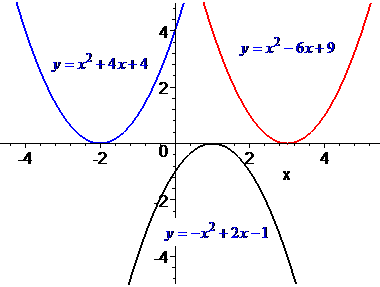
3) Останній випадок на практиці цікавий найбільше – існує дві точки перетину параболи з віссю абсцис. Це означає, що існує два дійсних кореня рівняння.

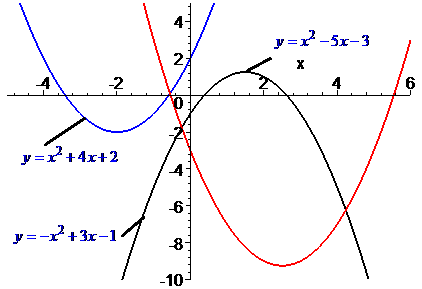
На основі аналізу коефіцієнтів при степенях змінних можна зробити цікаві висновки про розміщення параболи.

1) Якщо коефіцієнт а більший нуля то парабола направлена вітками вгору, якщо від'ємний — вітки параболи направлені вниз.

2) Якщо коефіцієнт b більший нуля то вершина параболи лежить в лівій півплощині, якщо приймає від'ємне значення – то в правій.

Виведення формули для розв'язування квадратного рівняння

Перенесемо константу із квадратного рівняння

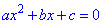
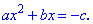
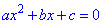
за знак рівності, отримаємо вираз

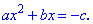
Помножимо обидві частини на 4а

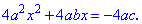
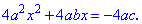
Щоб отримати зліва повний квадрат додамо в обох частинах b^2 та здійснимо перетворення

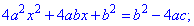
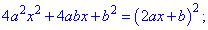
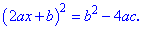
Звідси знаходимо

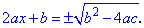
Формула дискримінанту та коренів квадратного рівняння

Дискримінантом називають значення підкореневого виразу

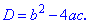
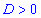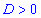Якщо він додатній  то рівняння має два дійсні корені, які обчислюють за формулою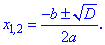

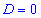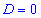При нульовому дискримінанті  квадратне рівняння має один розв'язок (два співпадаючих корені), які легко отримати з наведеної вище формули при D=0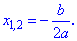

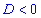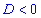При від'ємному дискримінанті  рівняння дійсних коренів немає. Однак ісують розв'язки квадратного рівняння в комплексній площині, і їх значення обчислюють за формулою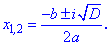

Теорема Вієта

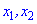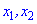Розглянемо два корені квадратного рівняння  та побудуємо на їх основі квадратне рівняння.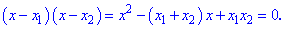

З запису легко слідує сама теорема Вієта: якщо маємо квадратне рівняння вигляду

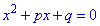
то сума його коренів рівна коефіцієнту p, взятому з протилежним знаком, а добуток коренів рівняння рівний вільному доданку q. Формулами сказане вище матиме такий запис

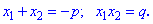
Якщо, в класичному рівнянні константа а відмінна від нуля, то потрібно поділити на неї все рівняння, а потім застосовувати теорему Вієта.

Розклад квадратного рівняння на множники

Нехай поставлено завдання: розкласти квадратне рівняння на множники. Для його виконання спочатку розв'язуємо рівняння (знаходимо корені). Далі, знайдені корені підставляємо в формулу розкладу квадратного рівняння

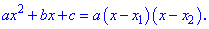
На цьому завдання буде розв'язаним.

Задачі на квадратне рівняння

Задача 1. Знайти корені квадратного рівняння

x^2-26x+120=0.

Розв'язання:

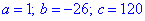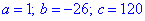Запишемо коефіцієнти  та підставимо в формулу дискримінанту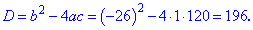

Корінь з даного значення рівний 14, його легко знайти з калькулятором, або запам'ятати при частому використанні, однак для зручності, вкінці статті я Вам дам список квадратів чисел, які найчастіше можуть зустрічатися при подібних задачах.

Знайдене значення підставляємо в формулу коренів

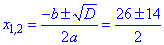
та отримуємо

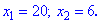
Задача 2. Розв'язати рівняння

2x^2+x-3=0.

Розв'язання:

Маємо повне квадратне рівняння, виписуємо коефіцієнти та знаходимо дискримінант

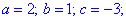
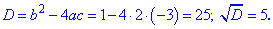
За відомими формулами знаходимо корені квадратного рівняння

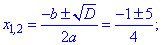
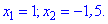
Задача 3. Розв'язати рівняння

9x^2-12x+4=0.

Розв'язання:

Маємо повне квадратне рівняння. Визначаємо дискримінант

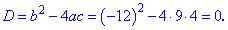
Отримали випадок коли корені співпадають. Знаходимо їх значення за формулою

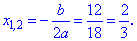
Задача 4. Розв'язати рівняння

x^2+x-6=0.

Розв'язання:

У випадках коли маємо малі коефіцієнти при х доцільно застосовувати теорему Вієта. За її умовою отримуємо два рівняння

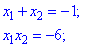
З другої умови маємо, що добуток має бути рівний -6. Це означає, що один з коренів від'ємний. Маємо наступну можливу пару розв'язків {-3;2}, {3;-2}. З врахуванням першої умови другу пару розв'язків відкидаємо.

Корені рівняння рівні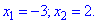 

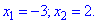
Задача 5. Знайти довжину сторін прямокутника, якщо його периметр 18см, а площа 77 см^2.

Розв'язання:

Півпериметр прямокутника дорівнює сумі сусідніх сторін. Позначимо х –більшу сторону, тоді 18-x менша його сторона. Площа прямокутника дорівнює добутку цих довжин:

х(18-х)=77;

або

х^2-18х+77=0.

Знайдемо дискримінант рівняння

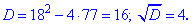
Обчислюємо корені рівняння

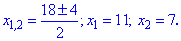
Якщо х=11, то 18-х=7, навпаки теж справедливо (якщо х=7 , то 21-х=9).

Задача 6. Розкласти квадратне 10x^2-11x+3=0 рівняння на множники.

Розв'язання:

Обчислимо корені рівняння, для цього знаходимо дискримінант

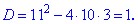
Підставляємо знайдене значення у формулу коренів та обчислюємо

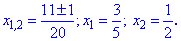
Застосовуємо формулу розкладу квадратного рівняння за коренями

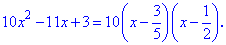
Розкривши дужки отримаємо тотожність.